De gulden snede in de kunst
Oefening 1
Een lijnstuk [AB] wordt door een punt M in twee delen verdeeld zodat de verhouding van het kortste stuk |MB| gelijk is aan de verhouding van het langste stuk |MB| tot het gehele lijnstuk |AB|. Bereken die verhouding eerst exact en dan numeriek tot op 3 cijfers na de komma.

Exacte berekening:
|AM| = |MB|
|MB| |AB|
Op de afbeelding zien we dat |AM| gelijk is aan 1 en dat |MB| gelijk is aan x. Het is de bedoeling dat we uitrekenen hoeveel keer groter |MB| is dan |AM|. Dit doen we door de formule in te vullen met de bovenstaande gegevens:
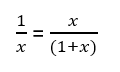
Als we deze formule uitrekenen, verkrijgen we een vierkantsvergelijking die we met de discriminant zullen uitrekenen.
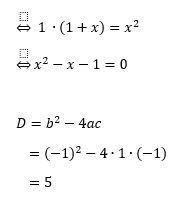
Aangezien de discriminant groter is dan 5, zijn er twee mogelijke oplossingen.
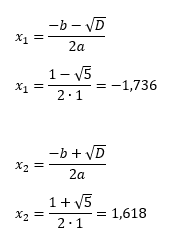
De eerste oplossing is niet mogelijk, aangezien de uitkomst negatief is. D.w.z. dat de verhouding tussen de twee lijnstukken 1,618 is of |MB| is 1,618 keer groter dan |AM|.
Oefening 2: Doryphoros
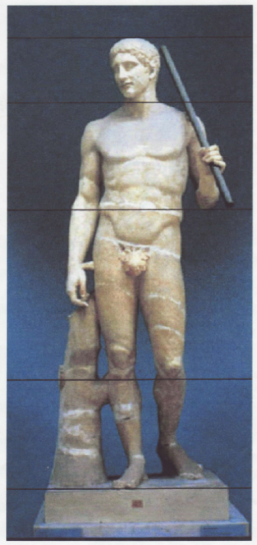
De griekste kunstenaar Polykleitos maakte omstreeks 450 voor Christus deze Doryphoros (speerwerper) om zijn theoretische werk te illustreren. Het gold jaren als voorbeeld van de ideale verhoudingen in het menselijk lichaam in de klassieke Griekse kunst. Het originele bronzen werk is verloren gegaan, maar er bestaan veel (meestal marmeren) kopieën uit de Romeinse tijd.
Meet de gevraagde afstanden en bereken de verhoudingen.
|
van voet tot navel |
12,6 cm = 1,615 7,8 cm |
|
van navel tot schouder |
5,9 cm = 1,513 3,9 cm |
|
van knie tot navel |
7,7 cm = 1,54 5 cm |
Oefening 3: De mens van Vetruvius
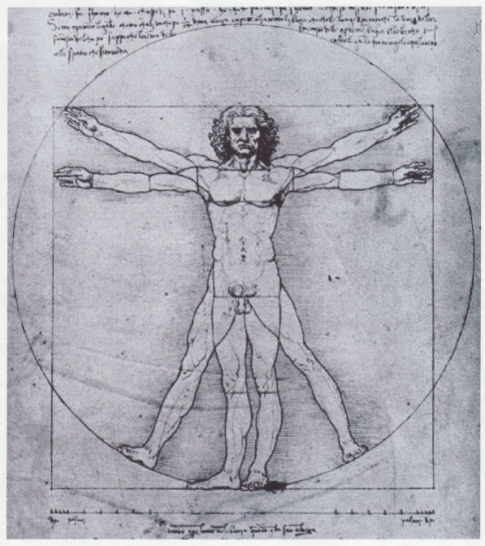
Zoals het in de Renaissance paste, bestudeerde Leonardo Da Vinci (1451 - 1519) de anatomie van het menselijk lichaam tot in het detail. Zijn studie van de geschriften van de Romeinse architect Vetruvius vormen daarvan een wereldberoemd hoogtepunt.
Meet de gevraagde afstanden en bereken de verhouding.
|
van voet tot navel |
8,6 cm = 1,509 5,7 cm |
Oefening 4: Mona Lisa

Leonardo Da Vinci (1451 - 1519) schilderde het portret van Mona Lisa (1479 - 1528), ook bekend als La Gioconda, de echtgenote van Francesco del Giocondo. Da Vinci schilderde de Mona Lisa met olieverf op hout tussen 1503 en 1506. Het schilderij(tje) van 77 x 53 cm bevindt zich in het Louvre in Parijs.
Bereken de verhouding van de breedte tot de lengte van het schilderij.
| lengte breedte |
77 cm = 1,45 53 cm |
De blikvanger van het schilderij is het gelaat van Mona Lisa, dat opvallend lichter van kleur is. Teken een rechthoek rond het gelaat. Bepaald de verhouding van de breedte tot de lengte van die rechthoek.
| lengte breedte |
6,5 cm = 1,625 4 cm |
Oefening 5: Het Laatste Avondmaal

Leonardo Da Vinci (1451 - 1519) werkte tot 1498 aan dit fresco in de eetzaal van het klooster Santa Maria della Grazie te Milaan. Dit werk is meer dan 4 meter hoog en 9 meter breed. Het plaaster heeft in de loop der tijden zó geleden, dat er van de oorspronkelijke schoonheid niet veel meer overblijft. De Abdij van Tongerlo bezit een mooi replica (op doek) uit 1545.
Kwatongen beweren dat dit fresco het huwelijk (!) van Jezus uitbeeldt. Zij motiveren dit door de bijzondere positie van de 'vrouwelijke' figuur die rechts van Jezus zit. Bepaal de verhouding van de delen links en rechts van deze figuur.
| rechts links |
15 cm = 1,63 9,2 cm |
Oefening 6: Norham Castle at Sunrise

De Engelse romantische schilder Joseph Mallord William Turner (1775 - 1851) staat bekend voor het gebruik van kleur en licht. Hij schilderde Norham Castle at Sunrise omstreeks 1835. Het doek van 78 x 122 cm bevindt zich in de Clore Gallery for the Turner Collection in Londen.
Het bruin-rode dier dat in het water staat, is een blikvanger van dit schilderij. Trek een verticale lijn door dit punt. Bereken de verhouding van de breedte van de twee delen waarin het schilderij door die lijn verdeeld wordt.
| links rechts |
15 cm = 1,63 9,2 cm |
Oefening 7: Une baignade à Asnières

De Franse neo-impressionist Seurat (1859 - 1891) schilderde de badgasten in zijn geliefde Asnières (een voorstad van Parijs) in 1883-84. Het werk bevindt zich in de National Gallery in London.
Teken een horizontale lijn volgens de blik van de jongen die over de Seine tuurt. Bepaal de verhouding van de hoogte van de delen waarin het schilderij hierdoor verdeeld wordt.
| onder boven |
9,5 cm = 1,53 6,2 cm |
Teken een verticale lijn door de ogen van de jongen. Bepaal de verhouding van de breedte van de delen waarin het schilderij hierdoor verdeeld wordt.
| onder boven |
9,5 cm = 1,53 6,2 cm |
Teken een verticale lijn door de ogen van de jongen. Bepaal de verhouding van de breedte van de delen waarin het schilderij hierdoor verdeeld wordt.
| links rechts |
14,8 cm = 1,49 9,9 cm |
Oefening 8: Het sacrament van het Laatste Avondmaal

De Spaanse kunstenaar Salvador Dalí (1904 - 1989) schilderde Het sacrament van het Laatste Avondmaal in 1955. Het bevindt zich in de National Gallery of Art in Washington.
Bepaal de verhouding van de hoogte tot de breedte van het schilderij.
| breedte hoogte |
24,2 cm = 1,613 15 cm |
Het tafelblad verdeelt het schilderij in twee delen. Bepaal de verhouding van de hoogten van deze delen.
| boven onder |
9,8 cm = 1,75 |
Trek een verticale lijn doorheen de figuur die rechts van Jezus Christus zit. Bepaal de verhouding van de breedte van de delen waarin het schilderij hierdoor verdeeld wordt.
| rechts links |
15 cm = 1,63 9,2 cm |
Oefening 9: Het Parthenon

Het Parthenon maakt deel uit van een groot heiligdom gelegen om een van de hoogste punten van de stad Athene: de Akropolis. De tempel is gebouwd tussen 448 en 432 voor Christus. De marmeren fries (de zogenaamde Elgin Marbles) werd in 1801 verwijderd en bevindt zich in The British Museum in London.
Doe alsof het fronton in de oorspronkelijke staat is. Bepaal de verhouding van de hoogte tot de breedte van het Parthenon.
| breedte hoogte |
14,6 cm = 1,62 9 cm |
Teken de horizontale lijn net boven de kapitelen (dus aan de onderzijde van het architraaf). Bepaal de verhouding waarin deze lijn het bouwwerk verdeelt.
| van grond tot kapitelen van architraaf tot fronton |
5,5 cm = 1,618 3,4 cm |
Teken de horizontale lijn onderaan de kroonlijst (die de fries met metopen en trigliefen scheidt van het fronton). Bepaal de verhouding waarin deze lijn het deel boven het architraaf verdeelt.
| kroonlijst en fronton architraaf en fries |
3,4 cm = 1,55 2,2 cm |
Een studie van dichterbij zou aantonen dat ook de verhouding van het architraaf tot de fries en de verhouding van de triptieken tot de metopen gelijk is aan de gulden snede.
Oefening 10
In oefeningen 1 tot en met 9 vind je telkens de zogenaamde gulden snede (of gouden verhouding)
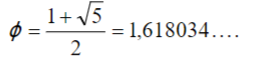


Oefening 11 a

Oefening 11 b

Stephanie Noben — stephanie
De gulden snede in de kunst - Laura — laura
De gulden snede in de kunst - Maxime — maxime
Kylie De Cuyper — kylie
