De gulden snede in de kunst - Maxime
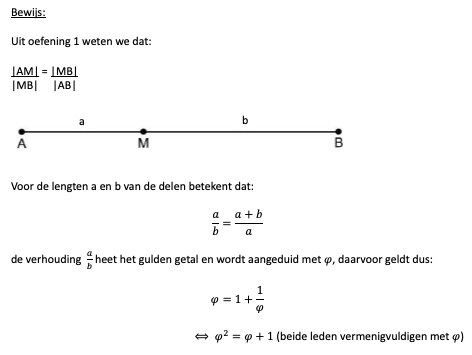
Oefening 1

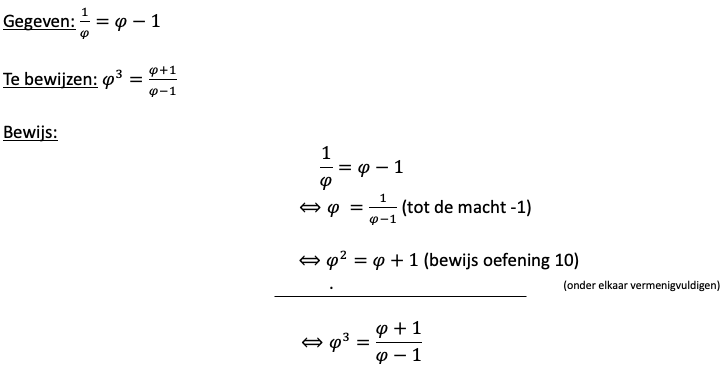
|AM| = |MB|
|MB| |AB|
Uit de afbeelding kunnen we halen dat |AM| gelijk is aan 1 en dat |MB| gelijk is aan x. We moeten uitrekenen hoeveel keer groter |MB| is dan |AM|. Dit gaan we doen door de formule in te vullen met de bovenstaande gegevens:
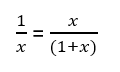
Als we kruiselings vermenigvuldigen, verkrijgen we de kruisproducten. Als we deze in één lid plaatsen krijgen we een tweedegraadsvergelijking, die we gaan oplossen aan de hand van discriminant.
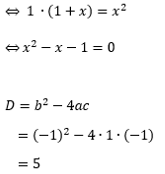
Aangezien de discriminant groter is dan 0, zijn er twee mogelijke oplossingen.
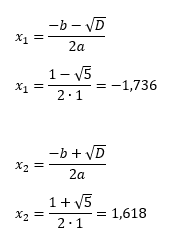
Omdat de eerste uitkomst negatief is, kan deze onmogelijk juist zijn. De tweede oplossing is wel positief, de verhouding tussen de twee lijnstukken is 1,618 of |MB| is 1,618 keer groter dan |AM|.
Oefening 2: Doryphoros
|
van voet tot navel |
12,4 cm = 1,62 7,65 cm |
|
van navel tot (linker)schouder |
4 cm = 1,38 2,9 cm |
|
van knie tot navel |
7,6 cm = 1,55 4,9 cm |
Oefening 3: De mens van Vetruvius
|
van voet tot navel |
8,6 cm = 1,54 5,6 cm |
Oefening 4: Mona Lisa
| lengte breedte |
77 cm = 1,45 53 cm |
| lengte breedte |
6,45 cm = 1,65 3,9 cm |
Oefening 5: Het Laatste Avondmaal
| rechts links |
14,8 cm = 1,63 9,1 cm |
Oefening 6: Norham Castle at Sunrise
| links rechts |
14,85 cm = 1,65 9 cm |
Oefening 7: Une baignade à Asnières
| onder boven |
9,4 cm = 1,54 6,1 cm |
| links rechts |
14,6 cm = 1,59 9,2 cm |
Oefening 8: Het sacrament van het Laatste Avondmaal
| breedte hoogte |
23,9 cm = 1,63 14,7 cm |
| boven onder |
9,2 cm = 1,67 |
| rechts links |
14,7 cm = 1,60 9,2 cm |
Oefening 9: Het Parthenon
| breedte hoogte |
14,5 cm = 1,61 9 cm |
| van grond tot kapitelen van architraaf tot fronton |
5,6 cm = 1,60 3,5 cm |
| kroonlijst en fronton architraaf en fries |
3,5 cm = 1,59 2,2 cm |
Oefening 10
In oefeningen 1 tot en met 9 vind je telkens de zogenaamde gulden snede (of gouden verhouding)
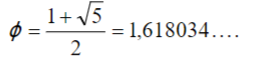

Oefening 11 a

Oefening 11 b