De gulden snede in de kunst - Laura
Oefening 1
Een lijnstuk [AB] wordt door een punt M in twee delen verdeeld zodat de verhouding van het kortste stuk |AM| tot het langste stuk |MB| gelijk is aan de verhouding van het langste stuk |MB| tot het gehele lijnstuk |AB|. Bereken die verhouding eerst exact en dan numeriek tot op 3 cijfers na de komma.

Oefening 2 Doryphoros

|
van voet tot navel van navel tot kruin |
12,6 = 1,615 7,8 |
|
van navel tot schouder van schouder tot kruin |
4,9 = 1,690 2,9 |
|
van knie tot navel van voet tot knie |
7,7 = 1,571 4,9 |
Oefening 3 De mens van Vetruvius
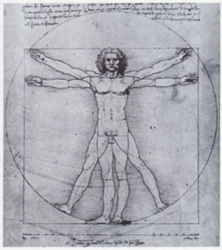
Meet de gevraagde afstanden en bereken de verhouding.
|
van voet tot navel van navel tot kruin |
9,6 = 1,684 5,7 |
Oefening 4 Mona Lisa

Bereken de verhouding van de breedte tot de lengte van het schilderij.
|
lengte breedte |
26,1 = 1,554 16,8 |
De blikvanger van het schilderij is het gelaat van Mona Lisa, dat opvallend lichter van kleur is.
Teken een rechthoek rond het gelaat. Bepaal de verhouding van de breedte tot de lengte van die rechthoek.
|
lengte breedte |
6,5 = 1,625 4 |
Oefening 5 Het Laatste Avondmaal

Kwatongen beweren dat dit fresco het huwelijk van Jezus uitbeeldt. Zij motiveren dit door de bijzondere positie van de ‘vrouwelijke’ figuur die rechts van Jezus zit. Bepaal de verhouding van de delen links en rechts van deze figuur.
|
rechts links |
15 = 1,630 9,2 |
Oefening 6 Norham Castle at Sunrise

Het bruinrode dier dat in het water staat, is een blikvanger van dit schilderij. Trek een verticale lijn door dit punt. Bereken de verhouding van de breedte van de twee delen waarin het schilderij door die lijn verdeeld wordt.
|
links rechts |
15 = 1,630 9,2 |
Oefening 7 Une Baignade à Asnières

Teken een horizontale lijn volgens de blik van de jongen die over de Seine tuurt.
Bepaal de verhouding van de hoogte van de delen waarin het schilderij hierdoor verdeeld wordt.
|
onder boven |
9,5 = 1,532 6,2 |
Teken een verticale lijn door de ogen van de jongen.
Bepaal de verhouding van de breedte van de delen waarin het schilderij hierdoor verdeeld wordt.
|
links rechts |
14,9 = 1,602 9,3 |
Oefening 8 Het sacrament van het Laatste Avondmaal

Bepaal de verhouding van de hoogte tot de breedte van het schilderij.
|
breedte hoogte |
24,2 = 1,613 15 |
Het tafelblad verdeelt het schilderij in twee delen. Bepaal de verhouding van de hoogten van deze delen.
|
boven onder |
9,4 = 1,679 5,6 |
Trek een verticale lijn doorheen de figuur die rechts van Jezus Christus zit. Bepaal de verhouding van de breedte van de delen waarin het schilderij hierdoor verdeeld wordt.
|
rechts links |
15 = 1,630 9,2 |
Oefening 9 Het Parthenon

Doe alsof het fronton in de oorspronkelijke staat is. Bepaal de verhouding van de hoogte tot de breedte van het Parthenon.
|
breedte hoogte |
14,6 = 1,622 9 |
Teken de horizontale lijn net boven de kapitelen (dus aan de onderzijde van het architraaf). Bepaal de verhouding waarin deze lijn het bouwwerk verdeelt.
|
van grond tot kapitelen van architraaf tot fronton |
5,5 = 1,618 3,4 |
Teken de horizontale lijn onderaan de kroonlijst (die de fries met metopen en trigliefen scheidt van het fronton). Bepaal de verhouding waarin deze lijn het deel boven het architraaf verdeelt.
|
kroonijst en fronton architraaf en fries |
15 = 1,630 9,2 |
Oefening 10
In oefeningen 1 tot en met 9 vind je telkens de zogenaamde gulden snede (of gouden verhouding)

Oefening 11

