Quickies in 3D

Voorbeeld 1

Oplossing: 

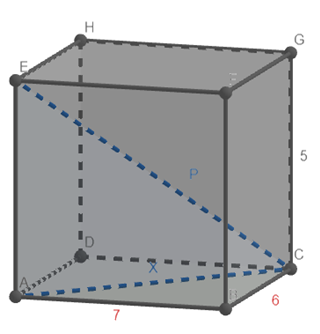
Het bewijs van de driedimensionale vorm is een kwestie van tweemaal de tweedimensionale stelling toepassen: eerst op het verticale diagonaalvlak door een opstaande ribbe c en een lichaamsdiagonaal d. Dat is een rechthoek met diagonaal d. Als e de horizontale zijde is van die rechthoek, geldt d² = e² + c² , terwijl e zelf voldoet aan e² = a² + b². Combinatie van de beide resultaten geeft a² + b² + c² = d² , zoals bewezen moest worden.

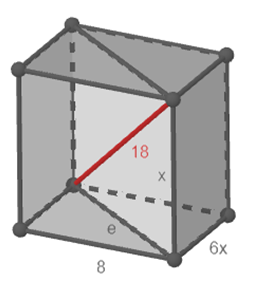
Gegevens invullen: x zoeken

$(6x)^2+ 8^2+ x^2= 18^2$

$36x^2+ 64 + x^2= 324$

$37x^2= 260$

$x^2=7.027$

$x = \sqrt{7.027}$

$x = 2.65$

Controle:

(6x)² + 8² + x² = 18²

(6· 2,65)² + 8² + 2,65² = 18²

252,81+ 64 + 7,03 = 324

Voorbeeld 2

Tekening/schets:

Oplossing:

Hoe bereken we de lengte van CE? In welke diagonaalvalk ligt CE?

Als we met ruimte figuren willen reken/werken willen de dit ruimte figuur altijd “plat” maken. Zorg daarvoor dat je een lijnstuk kiest waar CE in ligt.

In welke vlakken ligt het diagonaalvlak CE?

• Vlak ACGE
• Vlak CDEF
• Vlak EBCH

Een lichaamsdiagonaal ligt altijd in 3 diagonaalvlakken. Kies het diagonaalvlak waar je de meeste informatie van hebt.

We kiezen hier het diagonaalvlak ACGE.Omdat we hier met een balk werken is elk diagonaalvlak een rechthoek

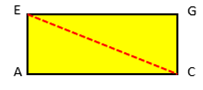
Hier kunnen we twee driehoeken van maken en passen we twee keer de stelling van Pythagoras toe.

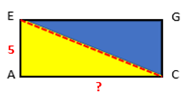
Voor we deze de stelling van Pythagoras toepassen is het belangrijk dat we de lengte van de zijden weten:

|AE| = 5 = hoogte van de balk

|AC| = ?

Hoe bereken we |AC|? AC bereken we via ∆ABC in het grondvlak:

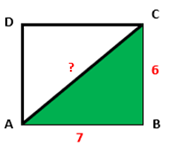
Omdat hier twee zijden bekend zijn kunnen we hier |AC| berekenen.

AC² = AB² + BC²

AC² = 7² + 6²

AC² = 85

AC = veriekantswortel(85) 

AC ≈ 9,2

Omdat we ook P willen weten reken we verder met de vorm AC² = 85

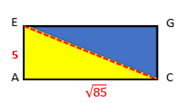
CE² = AE² + AC²

CE² = 5² + vierkantswortel (85)

CE² = 110

CE ≈ 10,49

Voorbeeld 3

Tekening/schets:

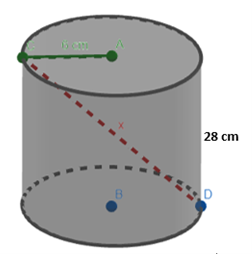
Oplossing:

1) We kunnen uit deze cilinder een driehoek halen.

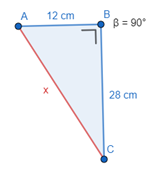
2) Hieruit kunnen we via de stelling van Stelling van Pythagoras: a² + b² = c² 

a² + b² = c²

12² + 28² = c²

144 + 784 = c²

928 = c²

c = 30,46 cm

Voorbeeld 4

Tekening/schets:

Oplossing:

Omdat we via de formule tangens de hoek willen berekenen hebben we eerst informatie nodig over de zijden.

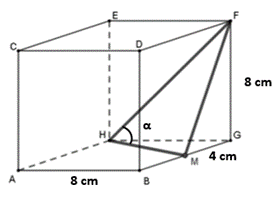
1. Bereken |FM|

Om |FM| te bereken kijken we naar de ∆FGM. Hier weten we al dat |FG| = 8cm en |GM| = 4cm, ook weten we dat hoek G een rechtehoek van 90 graden is (kubus).

Stelling van Pythagoras: a² + b² = c²

|FM|² = |FG|² + |GM|²

|FM|² = 8² + 4²

|FM|² = 64 + 16

|FM|² = 80

|FM|= 8,94 cm

2. Bereken |FH|

Hier kijken we naar het achtvlak van de kubus. Hier is |HF| de diagonaal van het vierkant EFGH. Dit kunnen we indelen in 2 driehoeken.

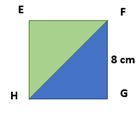
Hier weten we al dat |FG| = 8cm en |HG| = 8cm, ook weten we dat hoek G een rechte hoek van 90 graden is (kubus).

Stelling van Pythagoras: a² + b² = c²

|FH|² = |HG|² + |FG|²

|FH|² = 8² + 8²

|FH|² = 64 + 64

|FH|² = 128

|FH|= 11,31 cm

2. Bereken hoek α

Omdat we in de vorige stappen |FM| = overstaande zijden van α en |FH| = aanliggende zijden van α berekenden kunnen we nu ook hoek α berekenen door middel van de tangens formule.

Tan(∆HFM) = overstaande rechthoekzijden / aanliggende rechthoekzijden

Tan(∆HFM) = |FM| / |FH|

Tan(∆HFM) = vierkantswortel (80) / vierkantswortel (128)

Tan-1 (∆HFM)= 8,94 cm / 11,31 cm

Tan(∆HFM) ≈ 38,33 graden

Voorbeeld 5

Tekening/schets:

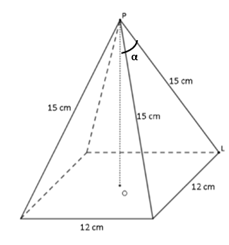
Oplossing:

1) Gegevens

|PL| = 15 cm

2) Bereken |LO|

Hier kijken we naar het grondvlak van de piramide. Hier is |LO| de diagonaal van het vierkant. Dit kunnen we indelen in 2 driehoeken.

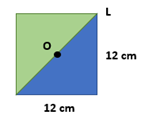
Hier weten we al dat de ribben van de kubus 12cm zijn.

Stelling van Pythagoras: a² + b² = c²

c² = b² + a²

c² = 12² + 12²

c² = 144 + 144

c² = 288

c ≈ 16,97 cm

Let op dit is de volledige zijden. We willen hier |LO| bereken en we weten dat O het middelpunt is van de diagonaal.

|LO| = 16,97 cm / 2 = 8,46 cm

3) Bereken hoek α

Omdat we in de vorige stappen |PL| = schuine zijden van α en |LO|= overstaande zijden van α berekenden kunnen we nu ook hoek α berekenen door middel van de sinus formule.

Sin(hoek α ) = overstaande rechthoekzijden / schuine zijden

Sin(hoek α ) = |PL| / |LO|

Sin(hoek α ) = 15 cm / vierkantswortel (288)

Sin^-1 (hoek α) = 15 cm / 16,97 cm

Sin(hoek α ) ≈ 62,12 graden