An Pacquée

Voorbeeld 1:

Gegeven:

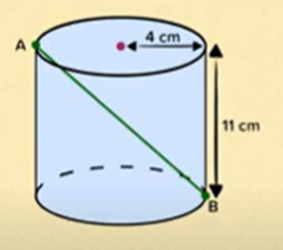
Gevraagd: Wat is de lengte van [AB]?

Oplossing:

Om deze lengte te kunnen berekenen, kunnen we eenvoudigweg van deze 3D-figuur een 2D-figuur maken door een schets te maken van een driehoek.

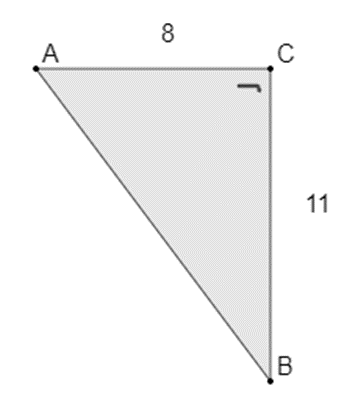
We weten dat de lengte van [BC] gelijk is aan 11 cm en dat [AC] de diameter is van de cirkel, dus is [AC] gelijk aan 8 cm.

Aan de hand van deze schets kunnen we de lengte van [AB] uitrekenen door gebruik te maken van de stelling van Pythagoras.

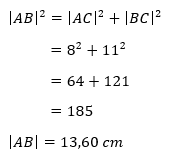
Voorbeeld 2:

Gegeven:

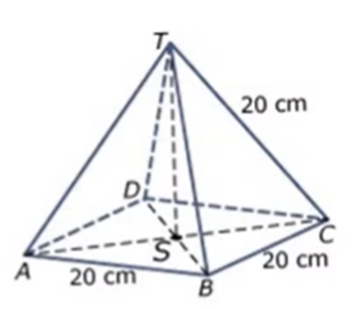
Gevraagd: Wat is de hoogte van deze piramide?

Oplossing:

Stap 1:

Om de hoogte van de piramide te kunnen berekenen, kunnen we gebruik maken van de stelling van Pythagoras. [TS] komt voor in driehoek ATC, waarvan we een schets maken.

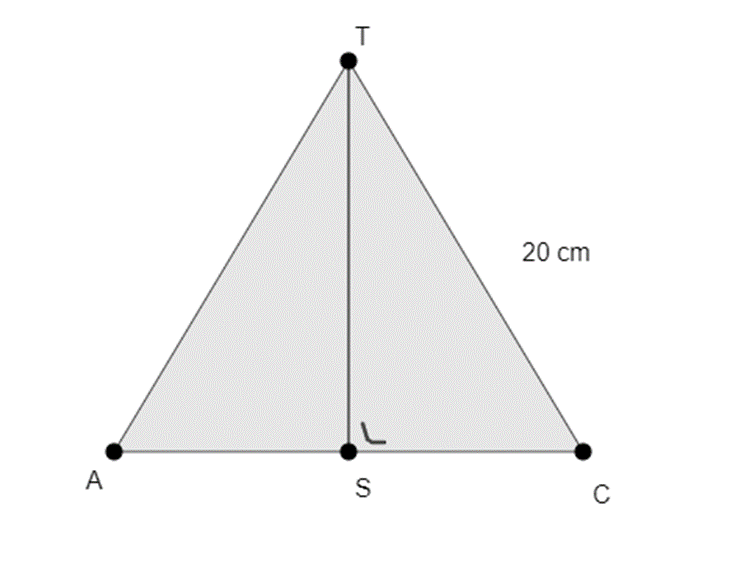
Stap 2:

We hebben nog te weinig gegevens om de berekening te kunnen uitvoeren. We moeten eerst nog uitrekenen wat de lengte van [CS] is. Deze zijde vinden we ook terug in het grondvlak van de piramide, waarvan we ook een schets tekenen.

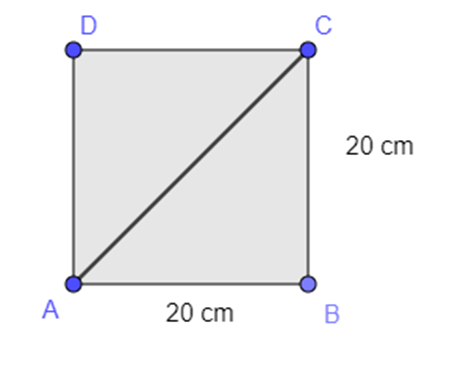
Nadat we de diagonaal AC getekend hebben, ontstaan er twee rechthoekige driehoeken en kunnen we de lengte van de schuime zijde AC uitrekenen door gebruik te maken van de stelling van Pythagoras. 

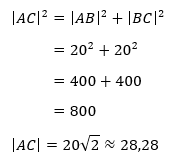
Stap 3:

We keren terug naar de schets van driehoek ATC. We weten nu wat de lengte van [AC] is. De lengte van [CS] is de helft errvan, dus 

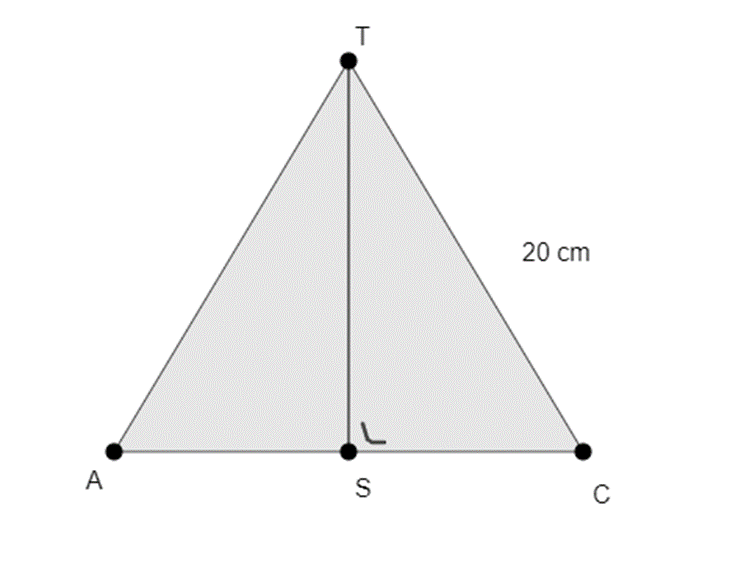
Nu hebben we voldoende gegevens om de lengte van [ST] te kunnen berekenen. Aangezien driehoek STC een rechthoekige driehoek is, kunnen we gebruik maken van de stelling van Pythagoras:

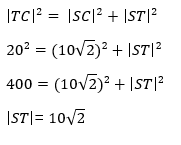
Voorbeeld 3

Gegeven:

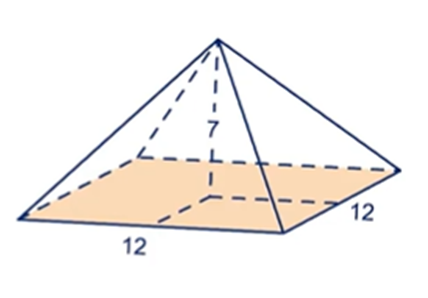
Gevraagd: Bereken de lengte van [TA]

Oplossing:

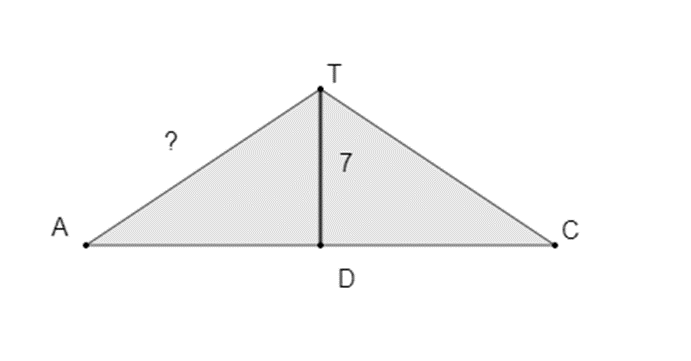
Omdat [TA] een zijde is van een driehoek, maken we een schets van driehoek ATC. [TD] is de middelloodlijn van de driehoek. Op die manier verkrijgen we twee rechthoekige driehoeken en kunnen we de lengte van [TA] berekenen met behulp van de stelling van Pythagoras. 
De lengte van [AC] kennen we nog niet, dus moeten wij deze eerst nog berekenen vooraleer we verder kunnen.

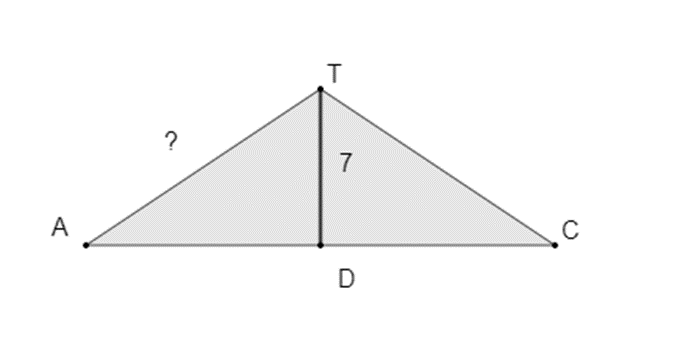
Stap 1:

[AC] komen we ook tegen in het grondvlak van de piramide. Via dit grondvlak kunnen we de lengte daarvan berekenen. We maken een schets van vierkant ABCD. 

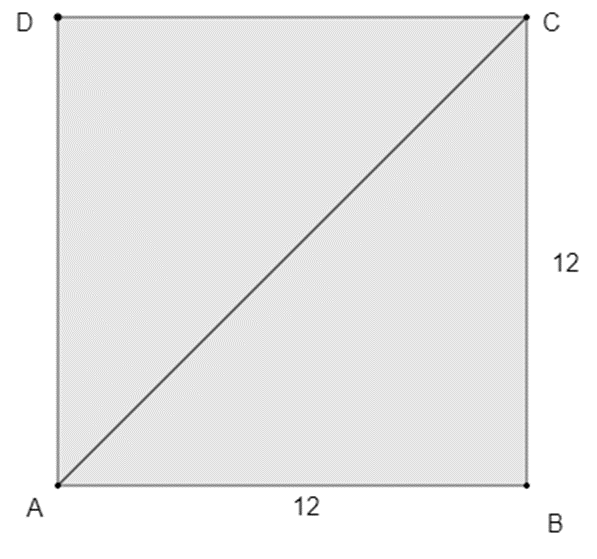
Omdat we de lengte van [AB] en [BC] kennen, kunnen we de lengte van [AC] berekenen met de stelling van Pythagoras:

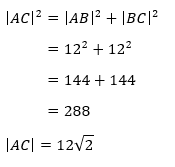
Stap 2:

We keren terug naar voorgaande schets.

Voorbeeld 4

Gegeven:

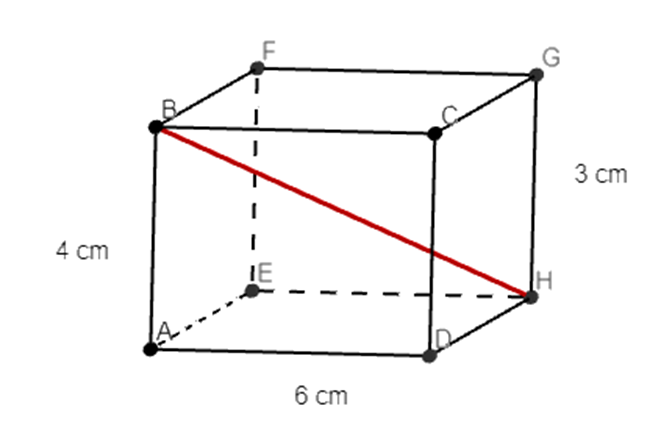
Gevraagd: Bereken de lengte van de lichaamsdiagonaal [EC] in cm. 

Oplossing:

Stap 1:

Deze balk is een ruimtefiguur. Om de berekening te kunnen maken van de lengte van [EC], zouden we van dit ruimtefiguur een 2D-figuur kunnen maken. [BG] ligt in het rechthoekig vlak ABGH.

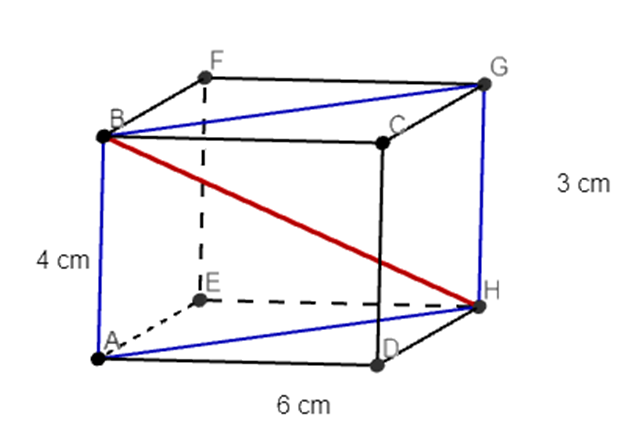
Stap 2:

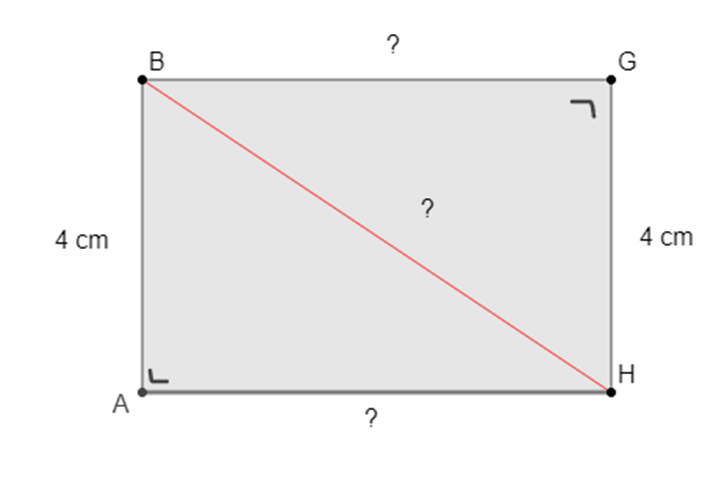
We tekenen het rechthoekig vlak ABGH zodat we een 2D-figuur bekomen.

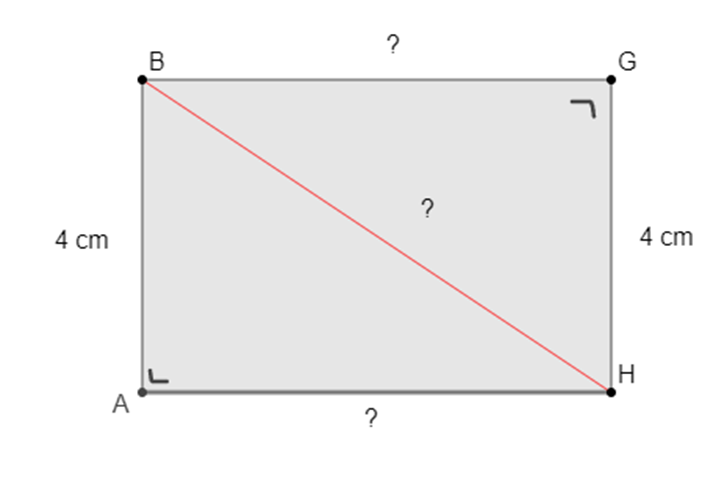
We weten dat [AB] een lengte heeft van 4 cm en dat [GH] 4 cm lang is. De lengte van [BG] en [AH] kennen we niet. We weten van  en ^G rechte hoeken zijn. 

Aangezien we de lengte van [BH] willen weten, verkrijgen we twee rechthoekige driehoeken waarvan [BH] de schuine zijde is. Als we de lengte van [AH] weten, zouden we de lengte van de schuine zijde kunnen uitrekenen met behulp van de stelling van Pythagoras.

Stap 3:

Om de lengte van [AH] uit te kunnen rekenen, moeten we op zoek gaan naar een ander vlak in het 3D-figuur, nl. AEHD, het grondvlak van de balk.

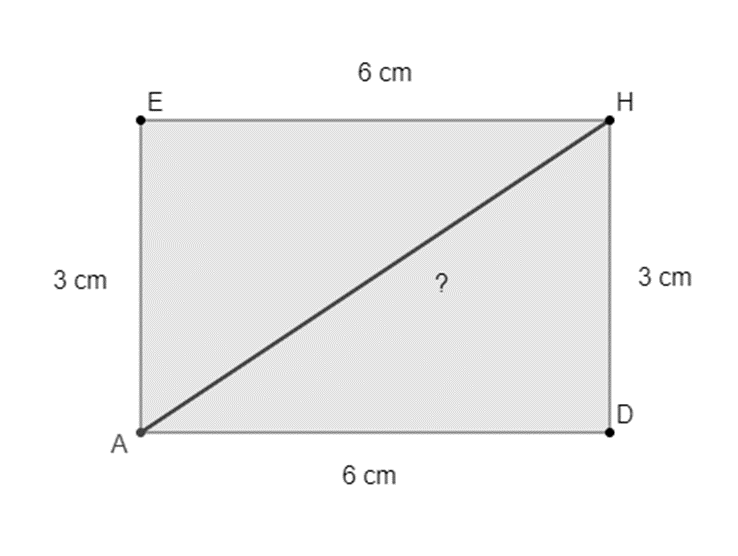
Omdat we de lengte van [AD] en de lengte van [HD] kennen, kunnen we [AH] uitrekenen a.d.h.v. de stelling van Pythagoras:

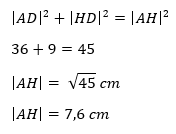
Nu we de lengte van [AH] kennen, kunnen we terugblikken naar de voorgaande figuur en kunnen we de lengte van [BH] uitrekenen, ook door gebruik te maken van de stelling van Pythagoras.

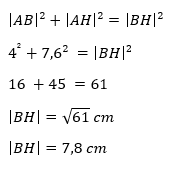
Voorbeeld 5

Gegeven:

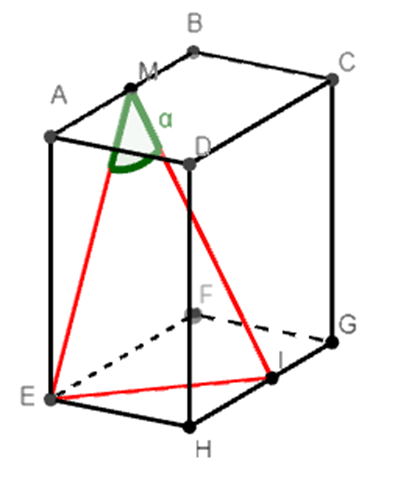
Gevraagd:

Bereken de hoek alpha.

Oplossing:

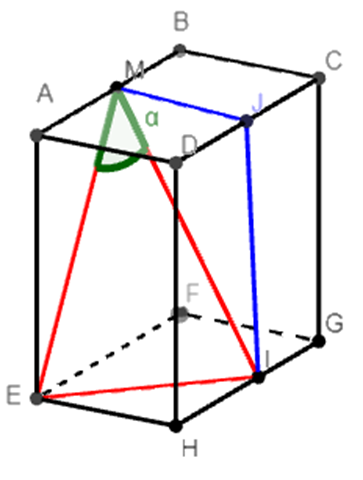
We zien in bovenstaand ruimtefiguur een driehoek. We kunnen deze oefening niet oplossen door enkel gebruik te maken van de stelling van Pythagoras, omdat deze driehoek geen rechthoekige driehoek is.

Aangezien we reeds enkele lengtes van zijden kennen en we op zoek moeten gaan naar de grootte van hoek alpha, kunnen we de cosinusregel toepassen:

Stap 1: Berekenen van de lengte [EI]

De lengte van [EI] kunnen we berekenen door gebruik te maken van de stelling van Pythagoras. We kennen de lengten van de andere zijden van driehoek EHI.

Volgende gegevens kennen we al:

[EH] is evenwijdig met [AD] en zijn beiden 3 cm lang.

De lengte van [HI] is de helft dan de lengte van [HG] (evenwijdig met [AB]) en is 2 cm lang.

Berekening:

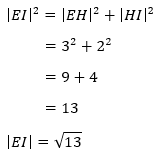
Stap 2: Berekenen van de lengte van [EM]

Ook de lengte van [EM] kunnen we berekenen met behulp van de stelling van Pythagoras. [EM] is een zijde van driehoek EAM, wat een rechthoekige driehoek is. 

Berekening:

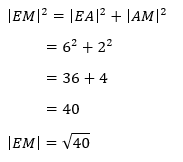
Stap 3: Berekenen van de lengte van [MI]

In bovenstaand ruimtefiguur zien we geen driehoek waarin de zijde [MI] voorkomt. Daarom tekenen we een nieuwe driehoek volgens onderstaand figuur: driehoek MIJ. Deze driehoek is een rechthoekige driehoek, dus kunnen we met de stelling van Pythagoras de lengte van [MI] berekenen.

Volgende gegevens kennen we al:

Stap 4: Cosinusregel in driehoek EMI

Met de gegevens die we net uitgerekend hebben, kunnen we nu alpha berekenen door middel  van de cosinusregel: