An Pacquée

Tijdschrift Pythagoras: Eerlijk delen

Voor deze opdracht heb ik de oefening eerlijk delen gekozen uit het tijdschrift Pythagoras januari 2016. Het was de bedoeling om een model van een dodecaëder te maken. Deze dodecaëder kan je in congruente figuren opdelen.

1. Benodigdheden

• Werkwijze uit het tijschrift Pythagoras januari 2016.
• Werkbladen uit het tijdschrift.
• Schaar.
• Plakband.

2. Werkwijze

Vooraleer ik aan deze opdracht kon beginnen, heb ik de online versie van het tijdschrift Pythagoras januari 2016 opgezocht en heb het artikel eerlijk delen gelezen.

Een dodecaëder of een regelmatig twaalfvlak is ruimtelijke figuur dat bestaat uit twaalf gelijkzijde vijfhoeken. Om dit te maken kon ik sjablonen downloaden.

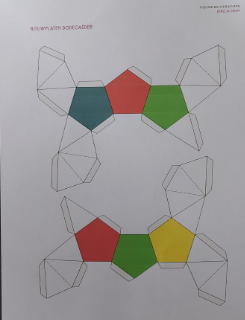
Door deze af te printen kon ik deze uitknippen en vouwen volgens de tekening in het tijdschrift. De prints werden in kleur afgeprint zodat er vijfhoeken ontstaan van 4 verschillende kleuren (zie foto's).

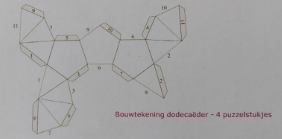
A.d.h.v. de nummers kon ik de flapjes telkens aan de juiste zijde aan elkaar kleven. Deze handeling moest ik vier keer uitvoeren. 

Als je de delen goed bekijkt, zie je dat de vijfhoek telkens bestaat uit een piramide. Elk deel bestaat uit drie piramides.

Op de foto kan je zien dat deze figuren, vier congruente fiiguren zijn. Ten slotte moesten deze figuren samengevoegd worden zodat een dodecaëder ontsaat.

Om ervoor te zorgen dat de aangrenzende vlakken niet dezelfde kleur hadden, moest ik de figuren meerdere keren in elkaar zetten om tot het gewenste resultaat te komen.

Wat liep er goed en wat minder goed?

Het was handig om de werkbladen af te printen zodat ik de juiste verhoudingen had om mee te werken. De knipbladen waren wel redelijk klein zodat het moeilijker werd om de figuren te vouwen. Als ik van plan zou zijn om deze opdracht door leerlingen te laten uitvoeren, zou ik de werkbladen uitvergroten, zodat het handiger is om te vouwen.